Latent Dynamics
By operating in a compressed representation of the environment, latent dynamics offer computational efficiency and scalability, enabling applications in robotics, autonomous systems, and beyond.
Three parts
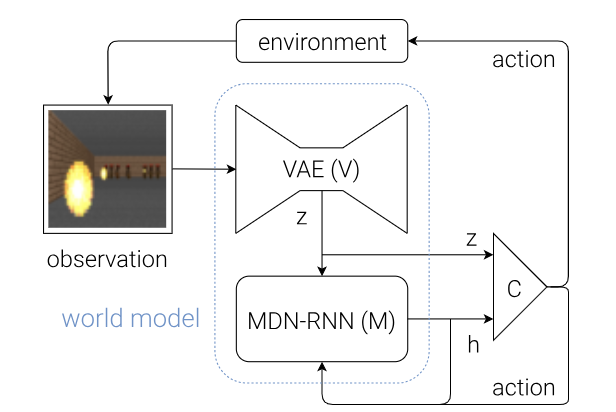
- VAE as a Vision model to encode a high dimensional 2D image at a time frame into a low dimensional latent vector[spatial compression].
- RNN model to make future prediction by compressing image data frames over time [temporal compression]. RNN needs to output stochastic prediction (in the form probability distribution p(z) instead of z) as complex environments are stochastic in nature. It is followed by a mixture density network (MDN) to estimate p(z) as a mixture of gaussian distributions.
- Finally, the controller model is responsible for deciding the action, it is a small, linear model trained with the Covariance-Matrix Adaptation Evolution Strategy.
$$
\begin{aligned}
Q^*_{M'} (s,a) &= Q^*_M(s, a) - \Phi(s) \\
V^*_{M'} (s,a) &= V^*_M(s, a) - \Phi(s)
\end{aligned}
$$